| Abstract |
Theoretical analysis of the controlled actuation of electroactive polymers with embedded high
dielectric nanoparticles will be presented. From experimental studies it is known that if the
inclusions are placed randomly in the elastomer body, the composite always contracts along the
direction of the applied electrostatic field E. This contraction is stronger than the
Maxwell-stress contraction because of the additional contraction stemming from the negative
electrostriction effect related to the dipole-dipole interactions between polarized inclusions.
Simulation results indicate that a similar negative electrostriction effect exists in simple cubic
(SC) regular lattice nanocomposites when the applied field is directed along the [001] direction of
the lattice. For inclusions occupying the sites of other lattice structures such as body-centered
(BCC) or face-centered cubic crystals (FCC), the composite elongates along the field direction if
it is applied along the [001] direction. The stability of the elongation against the imperfectness
of the lattice site positions and the distortion ratio of the initial structures are examined.
Finite elongation windows show up for the initially distorted BCC and FCC structures as a function
of the distortion ratio of the initial structure. The existence of these elongation windows are
also predicted from the analysis of the electrostatic energy of dipolar crystal structures.
Obtained results indicate that the electrostriction effect strongly depends on the geometry of the
spatial distribution of nanoparticles, and can thereby largely be tuned. An example of such
behavior is shown in Figure 1. Using different actuation responses of lattice and random
nanocomposites I propose to build artificial meta-structures which can bend, twist, or get
locomotive thrust under applied fields. In Figure 2 a bending-type meta-structure is shown. It has
a layered morphology with a gap between the regular lattice and random distributions for
inclusions. The existence of trapped charges at the inclusionelastomer interface makes the polymer
deformation in each layer dependent on the polarity of the applied field E. As a result of this,
the bending direction is different for positive (directed up) and negative (directed down) fields.
By changing the stacking morphology of such layers, or by putting vertical gaps inside the
distributions, it is possible to get a variety of deformations, including peristaltic wave and
twisting-bending mode responses.
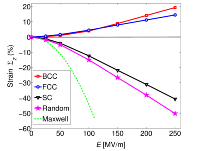
Fig.1 Nanocomposite deformation under the applied field E oriented in the [001] direction.
Four different spatial distributions for the inclusions, three regular lattice and one
random, are used. Shown is the deformation strain Σz as a function of applied field
E.
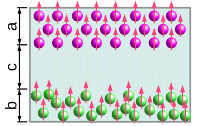
Fig.2 Schematic representation of a metastructure nanocomposite consisting of
a regular lattice distribution of a thickness a in the upper half, and a random
distribution of a thickness b in the bottom half of the layer, with a gap c between these
structures. |



