Direkt zu
Informationen für

 

 

 

 

 

Gefördert durch die

 

Ergebnisse

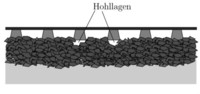
Zerkleinerungs- und Setzungsvorgänge bei Eisenbahnschotter.
Zerkleinerungs- und Setzungsvorgänge bei Eisenbahnschotter.

Die Diskrete-Elemente-Methode (DEM) wurde in der ersten Förderphase des Teilprojektes erfolgreich zur Simulation granularer Betten aus brechbaren Körpern eingesetzt. Es wurde eine Methodik entwickelt, die es erlaubt, aus brechbarem granularen Material realistisch geformte Steine aufzubauen und diese weitergehenden Analysen zu unterziehen. Bisher wurden hierbei entweder nur Kugeln bzw. Scheiben aus brechbarem Material [LM05, LGV06] oder unregelmäßig geformte nicht brechbare Steine verwendet [LM07]. Es lassen sich nun somit Vorgänge in Schotterbetten unter Berücksichtigung von Teilchenbrüchen simulativ untersuchen.

Zerkleinerungs- und Setzungsvorgänge bei Eisenbahnschotter.
Materialmodellierung als System verbundener Partikel.

Für eine Bewertung der Simulationsergebnisse wurden Vergleiche mit in der Literatur verfügbaren Experimenten [Die03, HB97, LID00, MC94] durchgeführt. Das Versagensverhalten harter Gesteinsmaterialien kann qualitativ sehr gut abgebildet werden. Auch sind einachsige und schwach dreiachsige Spannungszustände, wie sie in Schotterbetten vorliegen, gut quantitativ reproduzierbar. Vorteil der DEM ist, dass sich das Versagen allein aus der Belastung ergibt und eine Initialisierung der Risse nicht notwendig ist. Auch können mehrfache Brüche auftreten. Durch eine für die nächsten Förderperiode geplante Erweiterung der Bindungen soll die quantitative Abbildung der Festigkeit unter mehrachsiger Belastung weiter verbessert werden.

Literatur
Zerkleinerungs- und Setzungsvorgänge bei Eisenbahnschotter.
Definition von Tangentialebenen, die als Berandungsgeometrie der Makrokörper verwendet werden.

[LM05] W. L. Lim und G. R. McDowell. Discrete element modelling of railway ballast. Granular Matter, 7:19–29, 2005.

[LGV06] S. Lobo-Guerrero und L. E. Vallejo. Discrete element method analysis of railtrack ballast degradation during cyclic loading. Granular Matter, 8:195–204, 2006.

[LM07] M. Lu und G. R. McDowell. The importance of modelling ballast particle shape in the discrete element method. Granular Matter, 9:69–80, 2007.

[Die03] M. S. Diederichs. Rock fracture and collapse under low confinement conditions. Rock Mechanics and Rock Engineering, 36(5):339–381, 2003.

[HB97] E. Hoek und E. T. Brown. Practical estimates of rock mass strength. International Journal of Rock Mechanics & Mining Sciences, 34(8):1165–186, 1997.

[LID00] F. Lekarp, U. Isacsson und A. Dawson. State of the art. I: Resilient response of unbound aggregates. Journal of Transportation Engineering, 126(1):66–75, 2000.

[MC94] C. D. Martin und N. A. Chandler. The progressive fracture of lac du bonnet granite. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 31(6):643–659, 1994.