Ergebnisse
Dynamisch-adaptive Simulation einer lid-driven cavity
Als Ausgangspunkt einer skalierbaren Gitterbibliothek für dynamisch-adaptive, baum-strukturierte Gitter wurde die p4est Bibliothek gewählt und im Hinblick auf minimal invasive Integrationsfähigkeit optimiert. Dazu wurden random-access auf beliebige, direkte Nachbarzellen sowie sogenannte virtuelle Zellen eingeführt. Virtuelle Zellen sind Zellen ohne numerische Freiheitsgrade an Verfeinerungsgrenzen, die persistent Daten halten können, die auch im Ghostaustausch zwischen benachbarten Prozessoren berücksichtigt werden. Sie erlauben die Verwendung numerischer Algorithmen, die nur mit Nachbarzellen gleicher Größe zu interagieren.
 |
 |
|
Dynamisch-adaptive Simulation einer lid-driven cavity. Das initiale Gitter hat Diskretisierungslevel 3, [links|oben], dieses wird zu den Wänden hin bis Level 5 statisch verfeinert. Nach 2048 Zeitschritten erhalten wir mit dynamischer Adaptivität basierend auf Fluidgeschwindigkeit und Wirbelstärke das Gitter [rechts|unten]. |
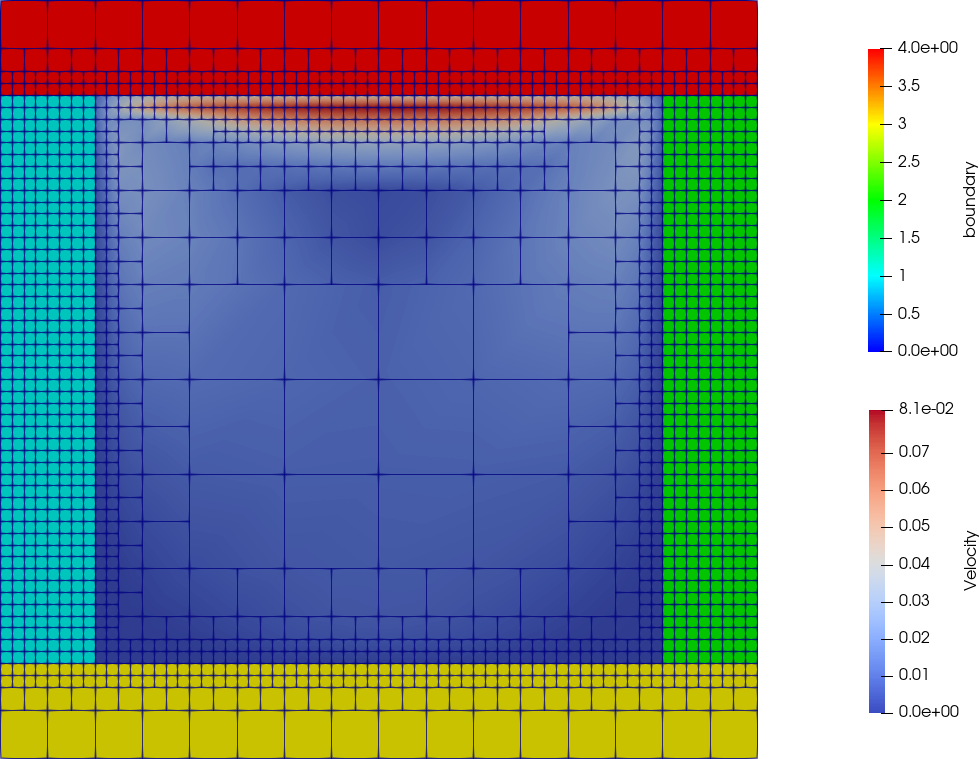 |
Diese erweiterte Version von p4est wurde schrittweise in ESPResSo integriert, so dass nun verschiedene physikalische Subsysteme auf einem p4est-basierten Gitter arbeiten können:
1. Kurzreichweitige Molekulardynamik zur Modellierung eines molekularen Ensembles.
2. Die lattice-Boltzmann Methode, um dieses Ensemble einer Hintergrundströmung auszusetzen.
3. Langreichweitige Molekulardynamik zur Modellierung elektrostatischer Interaktionen.
4. Das kontinuierliche Modell der Elektrokinetik zur Modellierung ionischer Fluide.
Die physikalisch richtige Kopplung der Subsysteme ist aktuell in Zusammenarbeit mit Teilprojekt C.5 in Arbeit.
Um den Aufwand der Kopplung möglichst gering zu halten, müssen alle zur Kopplung nötigen Informationen auf jedem Prozess lokal vorhanden sein. Daher wurden in enger Zusammenarbeit mit Teilprojekt D.9 Anforderungen und Algorithmen für die dynamische Änderung der Rechengitter und Prozessgrenzen, das heißt sowohl der lokalen Auflösung des Rechengitters als auch dessen Verteilung über die Prozesse, erarbeitet.
Erste Skalierbarkeitsmessungen für die lattice-Boltzmann Methode und die kurzreichweitige Molekulardynamik wurden auf Hazel Hen durchgeführt. In beiden Fällen erreichen wir gute Skalierbarkeit.

