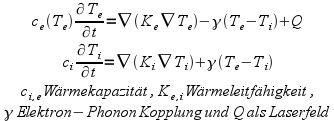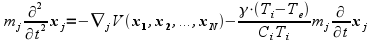Ergebnisse
Einleitung
Laserablation ist eine Technologie, die immer größere Bedeutung gewinnt beim Bohren, Erodieren, Schweißen, Strukturieren und Markieren aller Arten von Materialien. Modelliert wurde sie bisher meist mit Finite-Elemente-Verfahren. Dabei gehen Parameter ein, die aus dem experimentellen Studium grundlegender physikalischer Prozesse oder aus Simulationen bestimmt werden müssen. Für den industriellen Einsatz, werden üblicherweise Laserpulsdauern im Mikro- und Nanosekundenbereich verwendet. Das Material wird dabei aufgrund der entstehenden Schmelze und einsetzenden Wärmeleitung der Elektronen nahe der laserbearbeiteten Zone stark geschädigt. Es kommt zu Verstopfungen oder generellen Ungenauigkeiten der Strukturierung.
Mit dem Aufkommen ultrakurzer Pico- und vor allem Femtosekunden Pulse eröffneten sich eine Vielzahl neuer Bearbeitsungsmöglichkeiten. Der eigentliche Ablationsprozess ist dabei noch nicht verstanden. An dieser Stelle bieten sich Molekulardynamiksimulation an. Normalerweise ist es von Nachteil, dass Simulationen nur bis zum Nanosekundenbereich eingesetzt werden können. Dies ist aber gerade der interessante Bereich bei der atomistischen Simulation der Laserablation. Dazu wurde ein Verfahren in das Programmpaket IMD implementiert, mit dem das Laserlicht eingekoppelt und die Wärmeleitung durch die Elektronen beschrieben werden kann.
Technische Details
Die hier verwendete Methode ist eine Erweiterung des über 30 Jahre alten Zwei-Temperatur-Modells (TTM, two-temperature-model), das den Energietransfer innerhalb eines Metalls durch zwei gekoppelte Wärmeleitungsgleichungen für die Temperatur der Elektronen und des Gitters (Ionen) beschreibt:
|
|
Die Erweiterung besteht darin, dass die Phononendynamik nicht mittels einer gitterbasierten Methode gelöst wird, sondern mit standard Molekulardynamik, d.h. die Gleichung der Ionen wird durch die Lösung der Newtonschen Bewegungsgleichung ersetzt:
|
|
|
|
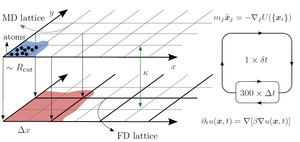
Das räumliche Gebiet wird zur Simulation in Molekulardynamikzellen (MD) eingeteilt. Diese Zellen wiederum werden in Finite-Differenzen (FD) Zellen gruppiert, in denen sich zwischen 100 und 1000 Atome befinden. Die Kantenlänge der MD-Zellen richtet sich nach der jeweiligen Potenzialreichweite (wenige Angström), die Menge an MD Zellen pro Finite-Differenzengitter wird durch die Menge an Atomen, die für eine statistische Temperaturerfassung notwendig sind nach unten begrenzt (Abb. 3).
Bei der Laserablation treten Phänomene auf, die sich mit den derzeit (2007) erhältlichen Finite-Elemente-Programmen nicht modellieren lassen. Insbesondere spielt es eine Rolle, ob das Material gasförmig, flüssig oder gar in festen Clustern abgetragen wird und dann mit dem Laserlicht wechselwirkt.
Erstes Qualitätskriterium für ein verwendetes Potenzial ist deshalb das Phasendiagramm. Als Modellsystem dient Aluminium, für das es bereits fertige EAM Potenziale in der Literatur gibt. Es wurden Wärmetransport- und Kapazitätsparameter bestimmt, Simulationen durchgeführt und die Ergebnisse mit dem Experiment verglichen (Abb. 4). Wie sich zeigt eignen sich nicht alle Potenziale für die Beschreibung bei hohen Temperaturen und Drücken – gerade der bei der Ablation interessante Bereich.
Simulationen
|
Für Simulationen werden zwei unterschiedliche Geometrien untersucht: zum einen Simulationen bei denen die komplette Probenoberfläche homogen bestrahlt wird. Dieser Prozess entspricht im Experiment dem Zentrum eines Laserpulses. Zum anderen untersuchen wir wie die Oberfläche auf inhomogene Strahlung, wie sie beispielsweise bei einer Gauss-Mode vorliegt, reagiert.
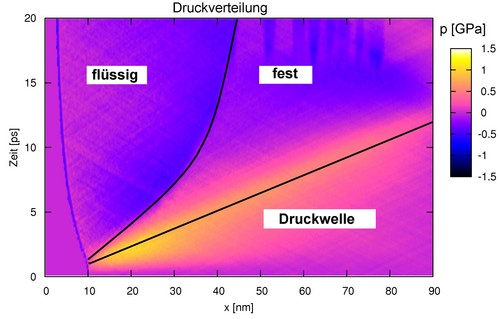
Aus der Molekulardynamiksimulation lassen sich Observablen wie Druck, (Gitter- wie auch Elektronen) Temperatur oder Dichte direkt bestimmen. Abb. 5 zeigt die Druckverteilung innerhalb der Probe: Noch während des Laserpuls beginnt das Material sich isochor zu erwärmen, das schnelle Ansteigen der Temperatur führt zu einer Druckwelle, die sich mit Schallgeschwindigkeit (~ 7km/s) ausbreitet. Gleichzeitig schmilzt das Metall nahe der Oberfläche, es bildet sich eine flüssig-fest Grenzfläche. Die vorliegende Simulation fand unterhalb der Ablationsschwelle statt, da kein Abdampfen von der Oberfläche zu sehen ist.
|
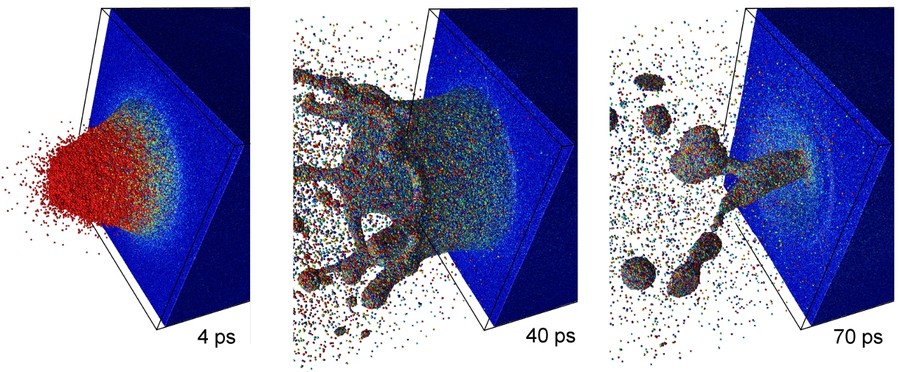
Für Simulationen mit inhomogener Laserstrahlung arbeiten wir zunächst mit einem phänomenologisch eingekoppelten Strahlungsfeld: Atome werden gemäß dem Lambert-Beerschen Gesetz angeregt. Die kinetische Energie wird dabei tiefenabhängig (exponentieller Abfall) reskaliert, so dass ein Impulsübertrag von Außen auf die oberflächennahen Atomschichten modelliert wird. Mittels Molekulardynamik können wir die Kraterentstehung beobachten (Abb. 5).
Außerhalb des SFBs besteht eine Kooperation mit dem Institut für Strahlwerkzeuge der Universität Stuttgart (IFSW), da dort sowohl Finite-Elemente-Rechnungen als auch Experimente der Laserablation durchgeführt werden und somit ein direkter Vergleich mit unseren Simulationen möglich ist. Derzeit rechnen wir Phasendiagramme für weitere Materialien wie Kupfer und Eisen. Weiter wird an Potenzialen für komplexere Systeme (Quasikristalle) gearbeitet. Diese Systeme bieten neben eines strukturreichen Phasendiagramms anisotrope Wärmeleitung und sind deshalb interessant für Studien zur Laserablation.
Innerhalb des SFB arbeiten wir mit dem Visualisierungsinstitut der Universität Stuttgart (VISUS) zusammen (D.3). Durch den engen Kontakt ist es möglich die Visualisierungstools direkt an unsere Simulation anzubinden um so die Daten schnell und effektiv auszuwerten (Abb. 6).

- Abbildung 6: Animation der Kraterentstehung (erstellt mit megamol).