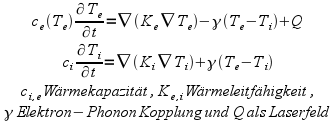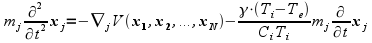Results
Introduction
Laser ablation is a technology gaining more and more importance with drilling, eroding, welding, structuring and marking all kinds of materials. It was modeled so far usually with finite element methods. The parameters usually used have to be determined by experimental studies of fundamental physical processes or by other simulations. For industrial applications, laser pulses lasting into the micro- and nanosecond range are used. Thereby, the material is strongly damaged due to the developing melt, beyond that, a fast thermal conduction of the electrons, which is typical for metals, close to the laser-affected zone leads to general inaccuracies of the structuring
With the introduction of ultrashort pico- and primarily femtosecond pulses, a multiplicity of new processing capabilities was opened. The actual ablation process is not yet understood. At this point, molecular dynamic simulation comes into consideration. Normally it is a disadvantage that simulations can be used only up to the nanoseconds, yet this is, however, the interesting range for the atomistic simulation of laser ablation. For that purpose, a method was implemented into the program IMD [2] which describes the coupling of the laser light and also the thermal conduction by the electrons.
Technical Details
The method used here is an extension of the over 30 years old two-temperature model (TTM) [1], which characterizes the energy transfer inside a metal by two generalized coupled heat conduction equations for the temperatures of the electrons and the lattice (ions):
|
|
The actual extension is a modification of the phonon dynamics: the equations are not solved by means of a lattice-based method, but with standard molecular dynamics [2], i.e. the equations of the ions are replaced by the solution of the Newton's equations of motion:
|
|
|
|
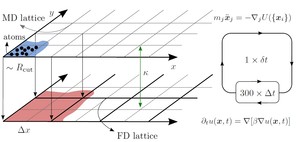
The spatial area is divided into so-called molecular dynamic cells (MD-cells). These cells again are grouped into finite-difference cells (FD-cells), to which between 100 and 1000 atoms belong to. The edge length of the MD-cells depends on the used potential range, the cut-off radius (few angstroms). The quantity of MD-cells per FD lattice is determined by the number of atoms which are necessary for a statistic temperature definition (fig. 3).
During the laser ablation, certain phenomena arise which cannot be modeled with the present (2007) available finite elements programs. In particular, important is whether the material is cleared away gaseously, in liquid form or in firm clusters. Even more, the ablated material itself may then interact with the laser light.
The phase diagram serves as a first quality criterion for the used potential. We used pure aluminum as model system, for which there are already finished EAM [3] potentials in the literature [4,5]. Heat transport and heat capacity parameters were determined, simulations accomplished and the results with the experiment (fig. 4) compared. It turns out, not all potentials for the description at high temperatures and pressures are suitable - the range interesting for the ablation process.
Simulations
|
Two different geometries were examined for the simulations: First, one for which the complete surface of the sample is illuminated homogenously. This process corresponds to the center of a laser pulse in an experimental setup. On the other hand we study how the surface reacts to inhomogeneous radiation, a beam profile present, for example, with a Gauss mode.
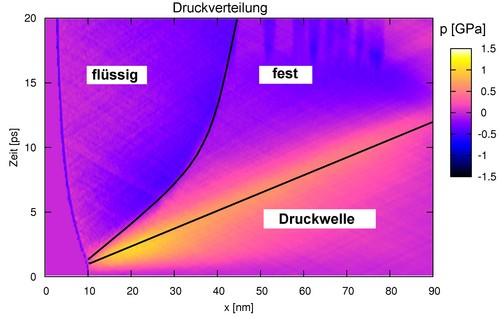
Several oberservables can be determined from the molecular dynamics simulation, such as the pressure, (lattice- and also electron-) temperatures or density. Fig. 4 shows the pressure distribution within the sample: during the laser pulse the material starts to heat up isochoric. The fast rise of the temperature leads to a pressure wave with speed of sound (~ 7km/s). At the same time, the metal close to the surface melts, it forms a liquid-solid boundary zone. The simulation took place below the ablation threshold, since no evaporation from the surface can be seen.
|
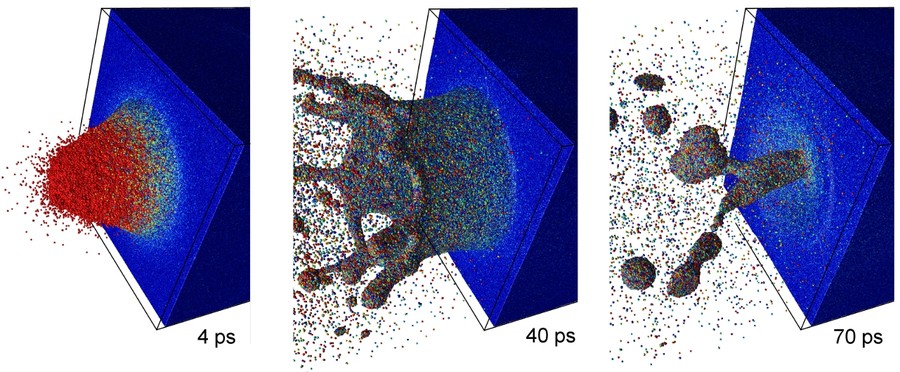
For simulations with inhomogeneous laser radiation, we use a more phenomenological approach for the coupling of the radiation field: the kinetic energy of the atoms is rescaled every time step according to Labert Beers Law, following an exponential decay. This way, an impulse-transfer from the outside on the atomic layers near the surface is modeled. By means of molecular dynamics, we can observe the crater emergence (fig. 5).
We cooperate with the Institut für Strahlwerkzeuge der Universität Stuttgart (IFSW) outside the SFB, since, both, finite element calculations and experiments of the laser ablation are performed there and, thus, a direct comparison with our simulations is possible. At present, we calculate phase diagrams for other materials such as copper and iron. We also work out potentials for more complex systems (quasicrystals). These systems offer, apart from a structural-rich phase diagram, anisotropic thermal conduction and are therefore interesting for studies of laser ablation.
Within the SFB, we work with the (VISUS), (project D.3). Due to the close contact, it is possible to directly use their visualization tools for our simulation, so that we can evaluate our data in a fast and effective way (fig. 6).

- Fig. 6: Laser Ablation in Metals