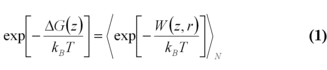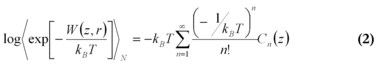Direkt zu
Informationen für

 

 

 

 

 

Gefördert durch die

 

Ergebnisse

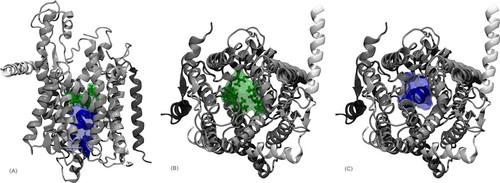
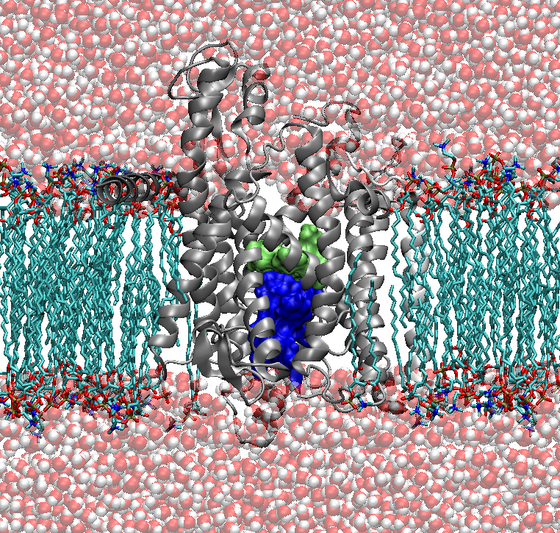
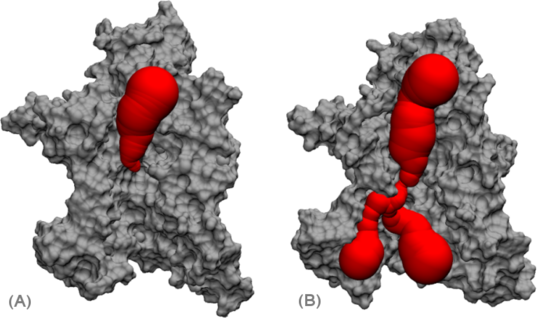
Abbildung1: Proteinkanal (SecYEβ-Komplex) in Cartoon Darstellung. Die einzelnen Untereinheiten sind in grau (SecY), dunkelgrau (Secβ) und hellgrau (SecE) weiß. In Liccorice- und transparenter Surface-Darstellung sind die Pore in grün und der Pfropfen in blau eingezeichnet. (A) Seitenansicht. (B) Aufsicht, mit hervorgehobener Pore. (C) Aufsicht, mit hervorgehobenem Pfropfen.

Ein Beispiel für einen natürlich vorkommenden Membrankanal ist der Protein-Translokations-Kanal SecYEβ. Dieser Kanal kann sowohl Proteine von einer Seite der Membran auf die andere schleusen, diese aber auch in die Membran einbauen. Zwei für die Funktion wichtige strukturelle Einheiten sind die Porenregion, ein Ring bestehend aus sechs hydrophoben Aminosäuren, und der sogenannte Pfropfen. Dieser besteht aus einer kurzen α-Helix, die sich direkt unterhalb der Pore befindet (Abb. 1).

Zur Proteintranslokation muss der Pfropfen aus der Porenregion entfernt werden und die Pore muss sich weiten. Beides garantiert die korrekte Funktion des Memrankanals, d. h. spezifischer Transport von Polypeptiden durch den Kanal auf der einen Seite, aber auch die Abdichtung des Kanals gegenüber Wasser, Ionen und anderen Molekülen im geschlossenen, inaktiven Zustand.

Aufgrund der verfügbaren Kristallstruktur des SecYEβ-Komplexes aus Methanococcus jannashii, die 2004 aufgelöst wurde [1], war es möglich Molekulardynamik-Simulationen an diesem System durchzuführen.

Aus der Analyse von EM-Daten eines Proteinkanal-Komplexes einer anderen Spezies (Sec61), zum einen mit gebundenem Ribosom und zum anderen ohne Bindungspartner, konnte darauf geschlossen werden, dass die Bindung an das Ribosom zu Konfor­mations­änderungen innerhalb der Proteinkanal-Struktur kommen muss, welche zu einer Herabsetzung der Bindungstärke des Pfropfens an die Pore führen könnte und somit einen Aktivierungs­prozess (öffnen des Proteinkanals) darstellen könnte [2-4].

Unter Verwendung neuerer EM-Daten in Kombination mit der vorhandenen Kristallstruktur, war es möglich eine Modellstruktur eines Sec61-Kanals gebunden an das Ribosom zu erstellen, sowohl in der inaktiven (2AKI), als auch in der aktiven (2AKH) Form [5].

Abbildung 2: Zeitskala unterschiedlicher chemischer und biologischer Prozesse. Intramolekulare Prozesse sind in grün, biologische Prozesse, die auch intermolekularer Natur sein können, sind in orange eingezeichnet. Heute realisierbare Simulationszeiten mit MD-Simulationen sind in rosa unterlegt. Der typische Integrationszeitschritt einer MD-Simulation (1 fs) ist in rot gekennzeichnet.

In diesem Teilprojekt werden all-atom Molekulardynamik-Simulationen, sowohl an der inaktiven als auch der aktiven Konformation des Proteinkanals SecYEβ durchgeführt, um im Detail den Funktionsmechanismus des Proteintransports über eine Membran zu verstehen und Fragen bezüglich Translokation, Abdichtung des Kanals und dem Relaxationsverhalten beantworten zu können. Hierbei ist unterschiedliches Verhalten zwischen aktiver und inak­tiver Form ein wesentlicher Aspekt auf den geachtet werden muss.

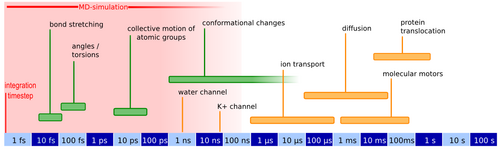
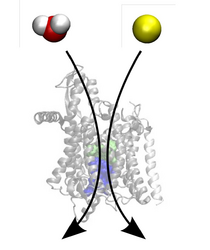
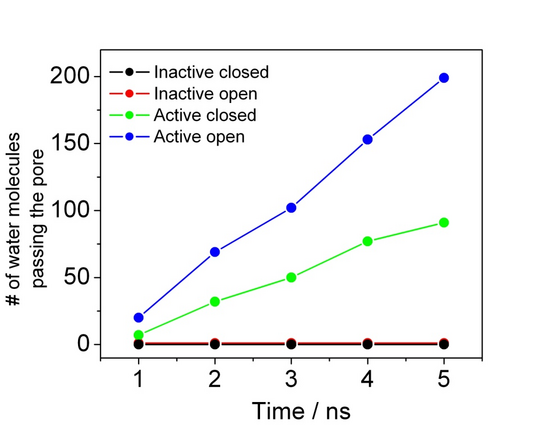
Die eben erwähnten Prozesse wie der Öffnungsmechanismus oder die Translokation von Polypeptiden und anderer molekularer Komponenten finden auf Zeitskalen statt, die von heutigen Standard-MD-Simulationen nicht abgedeckt werden können (Abbildung 2).

Daher ist es notwendig solche Prozesse auf die zur Verfügung stehende Simulationszeit zu beschleunigen. Dies lässt sich mit speziellen Methoden, wie beispielsweise SMD (Steered Molecular Dynamics) [6] bewerkstelligen. Aus den so entstandenen Nichtgleichgewichtsdaten müssen dann, beispielsweise mit Hilfe von Fluktuationstheoremen, die zugrunde liegenden interessierenden Gleichgewichtsgrößen, wie die Änderung der Freien Energie extrahiert werden.

Integrale Version des Fluktuationstheorems.

1997 formulierte Jarzynski eine integrale Version des Fluktuationstheorems, das die Änderung der Freien Energie ΔG mit einer exponentiellen Mittelung der von außen in das System eingebrachten Arbeit verbindet [7].

Hierbei ist W die Arbeit entlang einer Trajektorie und die spitzen Klammern deuten ein Ensemblemittel über N Trajektorien an.

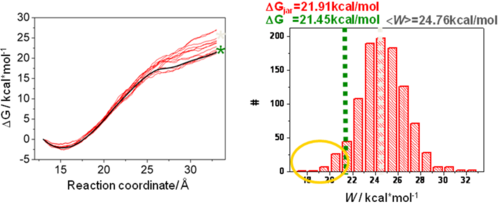
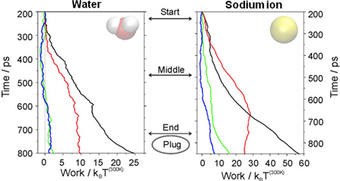
Abbildung 3: (A) Arbeitsprofile einer Anzahl an Trajektorien entlang einer Reaktionskoorindaten. Die Arbeitsprofile sind in rot, die mittlere Arbeit in hellgrau und die Änderung der Freien Energie ist in schwarz eingezeichnet.

Verwendet man unendlich viele Trajektorien ist die Gleichung exakt, für eine endliche Anzahl an Trajektorien erlaubt sie eine Abschätzung der Änderung der Freien Energie. Dies hängt stark davon ab, wie gut sich die Arbeitsverteilung mit den vorhandenen Daten beschreiben lässt. Abbildung 3A zeigt Arbeitsprofile einer Anzahl an Trajektorien, bei der sich das System während der Simulation nicht im Gleichgewicht befand. Die mittlere Arbeit ist hellgrau eingezeichnet und stets größer als die Änderung der Freien Energie (schwarz).

Unter Verwendung der Jarzynski-Gleichung (1) und einer Gesamtzahl von 1000 Trajektorien lässt sich die Änderung der Freien Energie sehr genau aus den Nichtgleichgewichtsdaten extrahieren (Abbildung 3B). Das Histogramm zeigt die Verteilung der Arbeitswerte am Ende der Reaktionskoordinaten. In grün ist der tatsächliche Wert angegeben, in rot die Abschätzung mit Hilfe der Jarzynski-Gleichung.

Das exponentielle Mittel der Arbeit in der Jarzynski-Gleichung (1) wird hauptsächlich von kleinen Arbeitswerten (gelber Kreis in Abbildung 3B) bestimmt. Diese Trajektorien treten jedoch sehr selten auf und führen dazu, dass das exponentielle Mittel sehr schwer abgeschätzt werden kann, wenn nur wenige Trajektorien zur Verfügung stehen oder das System weit aus dem Gleichgewicht getrieben wird. Dies führt dann zu einer Überschätzung der Änderung der Freien Energie.

Formulierung einer Näherung über die Jarzynski-Gleichung.

Im Fall von MD-Simulationen größerer Biomoleküle lässt sich aufgrund der notwendigen Rechenzeit nur eine geringe Anzahl an Trajektorien erzeugen, was eine direkte Anwendung der Jarzynski-Gleichung nur für Systeme nahe am Gleichgewicht möglich macht, d. h. die Arbeitsverteilung ist schmal (Breite der Verteilung σW ≈ kBT) [8]. Eine Näherung lässt sich formulieren, wenn man die rechte Seite der Jarzynski-Gleichung in eine Reihe von Kumulanten Cn(z) entwickelt.

Die Kumulanten Cn(z) aus Gleichung (2) beschreiben die Form der Arbeitsverteilung, z. B. C1=〈w〉 ist der Mittelwert, C2=〈w2〉-〈w〉2 die Varianz der Verteilung. Für den Spezialfall einer Normalverteilung der Arbeitswerte verschwinden alle höheren Terme der Reihe. In diesem Fall müssen nur der Mittelwert und die Varianz aus den Nichtgleichgewichtsdaten extrahiert werden. Dies ist auch für eine relativ kleine Anzahl an Trajektorien (ca. 10-20) und für Systeme, die nicht zu weit ins Nichtgleichgewicht getrieben wurden mit akzeptablem statistischen Fehler möglich.

Zusätzliches Bildmaterial

Abbildung 4: Zusammenbau der Startstruktur. Gezeigt ist eine Seitenansicht in der Membranebene. Das Protein ist in grau (Cartoon-Darstellung), die Pore und der Pfropfen sind in grün bzw. blau (Surface-Darstellung) eingezeichnet. Lipide und Wassermoleküle sind teilweise zur besseren Übersicht weggelassen.

Abbildung 5: Schematische Darstellung des Simulationsablaufs, bei der ein Wassermolekül bzw. Natrium-Ion durch die Membran gezogen wird. Wasser und Lipide sind zur besseren Übersicht nicht eingezeichnet.

Abbildung 6: Arbeitsprofile, um ein Wassermolekül bzw. ein Natrium-Ion durch den Kanalbereich zu ziehen.

Abbildung 7: Schnitt durch den Proteinakanal. Gezeigt ist eine Seitenansicht. Das Protein ist in Surface-Darstellung in grau gezeigt. Mögliche Wasserkanäle sind in rot eingezeichnet. (A) Inaktiv geschlossenen Konformation, (B) aktiv geschlossene Konformation. Während der Kanal im inaktiven Zustand abgedichtet ist, bilden sich im aktiven Zustand Wasserkanäle durch den Proteinkanal aus.

Abbildung 8: Anzahl an Wassermolekülen, die den Proteinkanal durchqueren. Unterschiedliche Konformationen wurden untersucht.
  

 

Referenzen

[1] van den Berg, B., et al., X-ray structure of a protein-conducting channel. Nature, 2004. 427 (6969): p. 36-44.

[2] Beckmann, R., et al., Alignment of conduits for the nascent polypeptide chain in the Ribosome-Sec61 complex. Science, 1997. 278 (5346): p. 2123-2126.

[3] Breyton, C., et al., Three-dimensional structure of the bacterial protein-translocation complex SecYEG. Nature, 2002. 418 (6898): p. 662-665.

[4] Menetret, J.F., et al., The structure of ribosome-channel complexes engaged in protein translocation. Molecular Cell, 2000. 6 (5): p. 1219-1232.

[5] Mitra, K., et al., Structure of the E-coli protein-conducting channel bound to a translating ribosome. Nature, 2005. 438 (7066): p. 318-324.

[6] Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered Molecular Dynamics and Mechanical Functions of Proteins. Curr. Opin. Struc. Biol. 11: 224-230.

[7] Jarzynski, C. 1997. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 78: 2690-2693.

[8] Park, S. and K. Schulten, Calculating potentials of mean force from steered molecular dynamics simulations. Journal of Chemical Physics, 2004. 120 (13): p. 5946-5961.