Ergebnisse
Das Arbeitspaket Interaktive Visualisierung zielt auf die Darstellung der unterschiedlichen Datendimensionen von Multiattributfeldern ab. Für die visuelle Analyse solcher Daten mit mehreren Attributen bietet sich die Kombination von Methoden der Informationsvisualisierung und der wissenschaftlichen Visualisierung an. Aus Sicht der Informationsvisualisierung sind Streudiagramme und parallele Koordinaten etablierte und effektive Methoden für multidimensionale Daten. Bisher standen diese Methoden jedoch nur für diskrete Daten zur Verfügung, d.h. für diskrete Datenpunkte ohne ein Modell einer räumlichen Rekonstruktion an Punkten, die nicht als Originaldatenpunkte vorliegen. Im Gegensatz dazu beruhen die Simulations- und Aggregationsergebnisse innerhalb des SFBs (und bei natur- und ingenieurwissenschaftlichen Simulationen im Allgemeinen) meist auf Modellen, die einen kontinuierlichen Berechnungsraum benutzen und damit die Möglichkeit zur Rekonstruktion von Zwischendatenpunkten implizieren. Aus diesem Grund stehen die bisher bekannten Verfahren für Streudiagramme und parallele Koordinaten schon auf der Modellebene nicht im Einklang mit den Datenmodellen. Daher wurden im Rahmen dieses Arbeitspakets das Konzept und die Verfahren für Streudiagramme und parallele Koordinaten modifiziert, so dass kontinuierliche Datensätze visualisiert werden können.
|
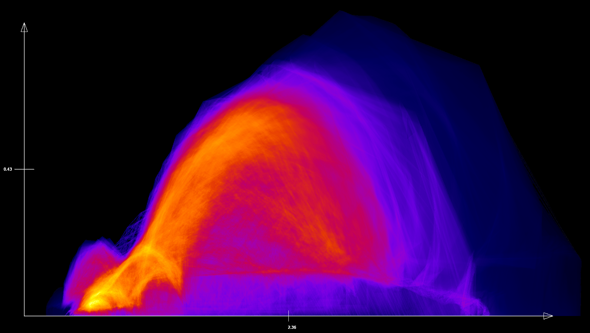
Bei kontinuierlichen Streudiagrammen (Abb. 1) werden nicht nur Gitterpunkt-Daten verwendet – wie es bei herkömmlichen, diskreten Streudiagrammen der Fall ist – sondern es werden Daten zwischen den Gitterpunkten interpoliert. Ein kontinuierliches Streudiagramm stellt also keine diskreten Datenwerte in Form von Punkten oder ähnlichen Glyphen dar, sondern für jeden Punkt des Diagramms wird die Dichte der Daten berechnet und als Farbwert kodiert dargestellt. Das zugehörige neue mathematische Modell für diese Dichten ist der Kern der Publikation. Die dort vorgeschlagene numerische Realisierung hat jedoch den Nachteil, dass nur eine lineare Interpolation für die Datenrekonstruktion unterstützt wird. Im Anschluss wurde dieses Verfahren weiterentwickelt, um nicht nur die Beschränkung auf die lineare Interpolation zu beseitigen, sondern auch eine Beschleunigung des Verfahrens zu erreichen. Diese Weiterentwicklung der kontinuierlichen Streudiagramme verwendet ein adaptives Verfahren, bei dem die Dichte, die im Streudiagramm dargestellt wird, nicht direkt berechnet, sondern durch einen Unterteilungsprozess angenähert wird. Dabei kann der Benutzer graduell zwischen einer hohen Darstellungsqualität oder einer schnellen Berechnung wählen. Es wird eine explizite Kontrolle des Approximationsfehlers unterstützt, und durch die Adaptivität skaliert unser Ansatz auch für große Datensätze. Im Gegensatz zum ursprünglichen Verfahren kann eine beliebige Interpolations- oder Rekonstruktionsmethode gewählt werden. Dies vermeidet Rekonstruktionsartefakte und führt zu einer Visualisierung, die konsistent mit dem Rekonstruktionsverfahren des Simulationsdatensatzes ist. Des Weiteren ist es bei diesem Verfahren möglich, eine effiziente hierarchische Datenstruktur zu verwenden (siehe auch Arbeitspaket Hierarchische Aggregation).
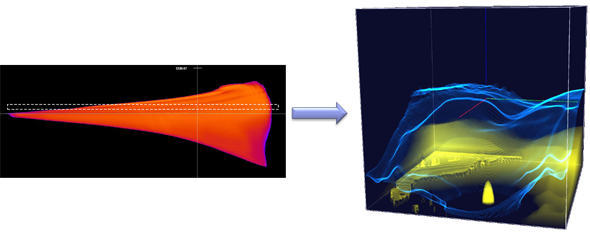
Alternativ zum hierarchischen Ansatz wurde eine parallele Implementierung für GPUs auf der Basis von CUDA (Compute Unified Device Architecture; eine vom GPU-Hersteller NVIDIA entwickelte Sprache für die effiziente Ausführung von nichtgraphischen Berechnungen auf GPUs) realisiert, womit eine substantielle Beschleunigung des ursprünglichen Verfahrens für stückweise linear interpolierte Daten und damit die Anwendbarkeit für große Datensätze erreicht wurde. Die Streudiagramme wurden darüber hinaus durch den Ansatz der koordinierten Mehrfachsichten (Multiple Coordinated Views) und des Brushing-und-Linking (dargestellt in Abb. 2) mit anderen Visualisierungssichten kombiniert – normalerweise mit klassischen Darstellungen aus der wissenschaftlichen Visualisierung. Eine typische alternative Visualisierungssicht ist die Volumenvisualisierung der räumlichen Verteilung eines Skalarfelds, beispielsweise der durch Aggregation gewonnenen Teilchendichten. Brushing erlaubt die Selektion von relevanten Datenmerkmalen im Streudiagramm durch graphische Interaktion (mittels Maus und Anklicken); Linking überführt diese Selektion automatisch auf eine entsprechende Selektion der zugehörigen Bereiche im räumlichen Datengitter.
|
Streudiagramme eignen sich hervorragend, um zwei Dimensionen eines Datensatzes zu analysieren. Falls ein Datensatz weitere Dimensionen enthält, können mehrere Streudiagramme für jeweils zwei Dimensionen erstellt werden, beispielsweise kombiniert in einer Streudiagramm-Matrix. Leider wird die Darstellung dadurch unübersichtlich und die gemeinsame, zusammenhängende Untersuchung mehrerer Dimensionen ist nicht möglich. Diese Limitierung kann durch den Einsatz von Diagrammen mit parallelen Koordinaten umgangen werden. Da die Methode der parallelen Koordinaten bisher nur für diskrete Datensätze konzipiert war, wurde hier derselbe Grundgedanke wie schon bei den Streudiagrammen verfolgt, um eine Erweiterung auf kontinuierliche Datenmodelle zu erreichen. In diesem Fall werden die diskreten Linien der parallelen Koordinaten auf ein Modell von Liniendichten erweitert. Zudem wurden mehrere alternative numerische Berechnungsverfahren vorgeschlagen, um die Darstellung von kontinuierlichen parallelen Koordinaten zu erzeugen.
|
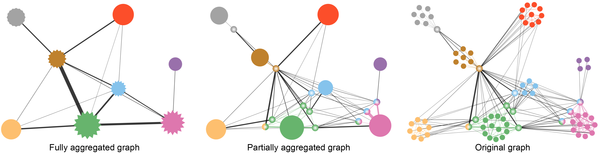
Netzwerk- bzw. Graphvisualisierungen werden häufig genutzt, um Relationen zwischen Objekten zu analysieren. Ein üblicher Ansatz dafür beruht auf Knoten-Kanten-Diagrammen, welche eine sehr einfache Navigation durch den Graphen erlauben, jedoch gleichzeitig für große Graphen (d.h. große Anzahl von Vertices und hohe Dichte von Kanten) aufgrund vieler Kantenkreuzungen unlesbar werden. Deshalb wurde die Graphvisualisierung hier um Methoden zur Aggregation und zum hierarchischen Clustering erweitert, mit denen eine deutlich bessere Skalierbarkeit erreicht werden konnte, d.h. es ist damit eine Multiskalenvisualisierung auf Graphen möglich. Das Besondere an dieser Arbeit ist die Unterstützung von Fuzzy-Clustering auf den Graphen: Graphvertices können mehreren Clustern zugeordnet sein, auch zu unterschiedlichen Graden. Hierdurch ist eine sehr flexible Strukturierung der Netzwerkhierarchie möglich (Abb. 3).
Übereinstimmung und Regression sind wichtig für eine multivariante Datenanalyse. Übereinstimmende Informationen werden typischerweise in Streudiagrammen visualisiert, während rückläufige Informationsübereinkunft durch Punkt-Linien-Zeichnungen in den Streudiagrammen dargestellt werden. Streudiagramme sind jedoch nicht in der Lage, übereinstimmende Informationen zu zeigen, die mehr als zwei Eigenschaften beinhalten. Um dieses Problem aufzuzeigen, haben wir indexierte parallele Koordinaten, z.B. eine Punkte-Darstellung, die lineare Übereinstimmungen zeigen kann (lineare Korrelation + Regression), für eine Roman-Visualisierungsmethode vorgeschlagen, die indexierte Punkte oberhalb von Polylinien im Bildraum von parallelen Koordinaten zeigt. Wie aus Abb. 4 ersichtlich, kann die Visualisierung von indexierten Punkten in parallelen Koordinaten nur lokale lineare Beziehungen für maximal drei Eigenschaften herstellen und zeigen, was in Streudiagrammen nicht möglich ist.
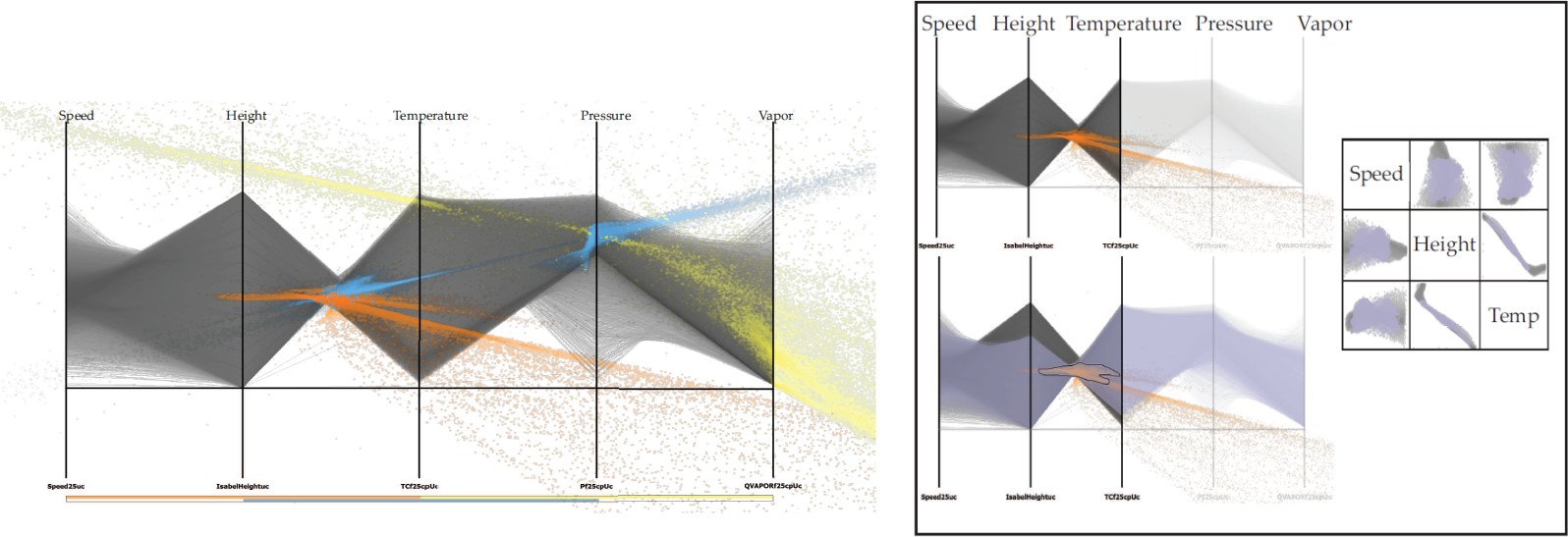
- Abb. 4: Die Visualisierung von indexierten parallelen Koordinaten zeigt lokale Verbindungen von Subspaces dreier ausgewählter Eigenschaften eines multivarianten Datensatzes (links). Über Brushing-und-Linking, einem Ebenen-Feature, können die Eigenschaften “Schnelligkeit”, “Höhe" und “Temperatur” visuell zueinander in Beziehung gesetzt werden (rechts).