Results
Im vorliegenden Teilprojekt werden sowohl vertikale als auch horizontale Kopplungsansätze verfolgt. Daher wurden detaillierte Studien mit Hilfe der Gitter-Boltzmann-Methode durchgeführt, die es erlauben, das Phänomen des Wandschlupfes besser zu verstehen und die existierenden mesoskopischen Modelle zu erweitern.
Zu den im Rahmen des SFB 716 durchgeführten Arbeiten zählt die Entwicklung neuer Ansätze innerhalb der Gitter-Boltzmann-Methode zur Simulation von Strömungen an hydrophoben, rauhen oder superhydrophoben Wänden. Diese Arbeiten haben zu zahlreichen Publikationen geführt und dienen als direkte Grundlage für die Entwicklung der Kopplungslgorithmen, die im Fokus des Teilprojekts stehen.
Die hier vorgestellten Arbeiten haben in großem Maße von einer engen Kollaboration mit dem Teilprojekt B.3 profitiert. Hier wurde gemeinsam die Genauigkeit der Gitter-Boltzmann-Methode in komplexen Geometrien, wie sie nicht nur in der Mikrofluidik, sondern auch in porösen Medien vorkommen, untersucht.
Es besteht eine enge Zusammenarbeit mit dem Teilprojekt A.1. Hier werden durch Molekulardynamiksimulationen erhaltene Kontaktwinkelmessungen eines Tropfens in einer Kapillare quantitativ mit Gitter-Boltzmann-Simulationen verglichen und für die Weiterentwicklung der mesoskopischen Modelle zur Beschreibung von Fluid-Wand-Wechselwirkungen verwendet. Dadurch ist eine vertikale Kopplung der verschiedenen Simulationsalgorithmen möglich, da ein direkter Zusammenhang zwischen den Parametern der Molekulardynamik und den Modellparametern der Gitter-Boltzmann-Methode gefunden wurde.
|
|
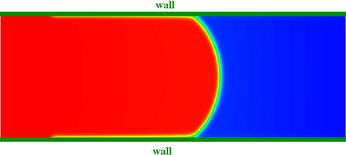
Abbildung 1 zeigt ein Beispiel von im Rahmen eine Kollaboration mit Teilprojekt A.1 simulierten Tropfen in einer Kapillare. Da die im Rahmen des SFB 716 entwickelten Methoden zur Fluid-Wand-Wechselwirkung innerhalb der Gitter-Boltzmann-Methode auf einem phänomenologischen Modell aufbauen, ist es notwendig, dieses Modell quantitativ mit Daten aus Molekulardynamiksimulationen zu eichen. Im vorliegenden Teilprojekt findet dies mittels einer Messung des Kontaktwinkels statt. Hierdurch ist es möglich, die auf Truncated-Shifted Lennard-Jones-Potenzialen basierende Beschreibung von Flüssigkeit und Gas auf das Shan-Chen-Mehrkomponenten-Gitter-Boltzmann-Modell zu übertragen.
Es hat sich gezeigt, dass die Molekulardynamik besonders im Bereich großer Dichteunterschiede der einzelnen Phasen funktioniert, während die Anwendbarkeit des Gitter-Boltzmann-Ansatzes hauptsächlich im für die Molekulardynamik schwer erreichbaren Bereich geringer Dichteunterschiede nahe der kritischen Temperatur liegt. Beide Methoden sind also komplementär und ergänzen sich durch ihre Anwendbarkeit in unterschiedlichen Parameterbereichen.
Die sogenannte horizontale Kopplung der Molekulardynamik wird sowohl mit einer teilchenbasierten mesoskopischen Methode (Stochastische Rotationsdynamik) als auch mit einer Kontinuumsmethode (Gitter Boltzmann) durchgeführt.
|
|
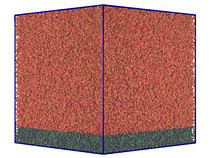
Im Rahmen der Stochastischen Rotationsdynamik kann der Kopplungsalgorithmus darauf beschränkt werden, dass die Teilchen in verschiedenen Simulationsvolumina unterschiedlich wechselwirken. Im vorliegenden Fall werden die in der Molekulardynamik wirkenden Potenziale an der Grenzfläche langsam aus- bzw. eingeblendet. Abbildung 2 zeigt ein Beispiel einer solchen Simulation.
Im Falle einer horizontalen Kopplung zwischen Molekulardynamik und Gitter Boltzmann muss ein geeigneter Übergang von der Teilchen- zur Kontinuumsbeschreibung gefunden werden. Dies geschieht mit Hilfe neu entwickelter Flussrandbedingungen an einer dünnen Grenzfläche zwischen beiden Simulationsvolumina. Für Molekulardynamik Teilchen, die in das Gitter Boltzmann Gebiet strömen, wurden neue Flussrandbedingungen für Gitter Boltzmann entwickelt, was zu einer ersten Publikation geführt hat. Strömungen vom Kontinuum in das durch Teilchen beschriebene Gebiet sind wesentlich schwieriger umzusetzen. Hier wird der sogenannte USHER Algorithmus verwendet um neue Teilchen an energetisch günstigen Punkten im Gebiet der Molekulardynamik zu erzeugen. Da dieser Algorithmus extrem rechenaufwändig ist, werden neue Parallelisierungs- und Optimierungsstrategien entwickelt.